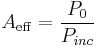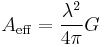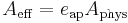Antenna effective area

In telecommunications, antenna effective area or effective aperture expresses an antenna's ability to collect an incident radio wave and deliver it as an electrical current at the antenna's terminals. The symbol A_eff is used to represent this figure, usually expressed in square meters.

Effective area is calculated using this formula:

$A_{\mathrm{eff}} = \frac{P_0}{P_{inc}}$

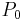Where $P_0$ is the power (usually watts) delivered by the antenna, and 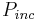$P_{inc}$ is the incident power density (usually watts per square meter) passing the antenna. It is assumed that the antenna is terminated with a matched load to absorb the maximum power.^[1]

For example, if an antenna delivers 30 watts of electrical power at its terminals when in the presence of electromagnetic waves whose density is 20 watts per square meter, then the antenna's effective area is 1.5 square meters.

1 Relationship to antenna gain
2 Relationship to physical area
- 2.1 Wire antennas
- 2.2 Aperture antennas
3 References
4 See also

Relationship to antenna gain

An antenna's effective area depends on its power gain. This is so because an antenna's power gain expresses two of its radiative physical properties: its directivity and its efficiency. Directivity describes its preference for certain angles of incidence, and efficiency describes the electrical losses inside it (due to ohmic resistance, losses into the surrounding dielectric, and similar). Both affect an antenna's effective area because both impact the power ultimately delivered at its terminals.

This formula calculates effective area as a function of its power gain:

$A_{\mathrm{eff}} = \frac{\lambda^2}{4\pi}G$

where G is the antenna's power gain (not its relative gain or dBi), and $\lambda$ is the wavelength.

That formula can be derived as a consequence of electromagnetic reciprocity which relates the transmit properties of an antenna to the receiving properties. Consequently, it may not hold if the antenna is made with certain non-reciprocal materials.

Like the power gain property on which the equation depends, the effective area varies with direction. If no direction is specified, the direction that produces the maximum gain and maximum effective area is assumed.

Relationship to physical area

Simply increasing the size of antenna does not guarantee an increase in effective area; however, other factors being equal, antennas with higher effective areas are generally larger.

Wire antennas

In the case of wire antennas, there is no simple relationship between physical area and effective area. However, the effective areas for wavelength $\lambda$ of well-known wire antennas can be calculated from their (constant) power gain figures^[2]:

Wire antenna	Power gain	Effective area
Short dipole aka Hertzian dipole	1.5	0.1194 $\lambda$ ²
Half-wave dipole	1.64	0.1305 $\lambda$ ²
Monopole* aka Quarter-wave	3.28**	0.2610 $\lambda$ ²

Assuming the monopole antenna has an infinite ground/counterpoise.

Monopoles have twice the power gain of dipoles because they do not radiate into the space below their ground plane.

Aperture antennas

In the case of aperture antennas (horns and parabolic reflectors) considered in their direction of maximum radiation, the aperture efficiency is the ratio of effective area to physical area:

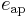$A_{\mathrm{eff}} = e_{\mathrm{ap}} A_{\mathrm{phys}}$

where $e_{\mathrm{ap}}$ is the aperture efficiency, 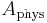$A_{\mathrm{phys}}$ is the physical size of the aperture, and 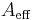$A_{\mathrm{eff}}$ is the effective aperture.

Federal Standard 1037C implies that the aperture efficiency is 0.35 to 0.55, which is true for simple designs. However, carefully designed and constructed reflector antennas can easily have efficiencies in the 0.65 to 0.75 range, and values as high as 0.85 have been reported in the literature. However, very high aperture efficiency is not always desirable because such antennas tend to have large side lobes.

Factors limiting the aperture efficiency are non uniform illumination of the aperture, phase variations of the aperture field (typically due to surface errors in a reflector and high flare angle in horns), and scattering from obstructions. The incident wavefront may also not be completely phase coherent due to variations in the propagating medium; this results in an increase in the effective area of an antenna not resulting in a commensurate increase in signal power, an effect known as 'aperture loss'.

References

^ Federal Standard 1037C
^ Orfanidis, Sophocles J. (2010) Electromagnetic Waves and Antennas chapter 15 page 609, retrieved 2011-04-05 from http://www.ece.rutgers.edu/~orfanidi/ewa/